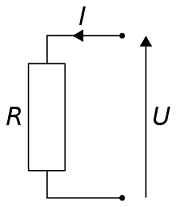
Loi d'ohm
|
U = R X I Avec:
|
Exercice 1 : Calcul de la tension aux bornes d'une résistance (loi d'ohm)
Soit une résistance de 22kΩ traversé par un courant de 5mA. Quelle est la valeur de la tension aux bornes de cette résistances?
Il faut faire attention aux unités ici. 22 kΩ = 22.103 Ω et 0,5 mA = 0,5.10-3A.
On peut donc calculer U = 22.103 X 0,5.10-3 = 11 V.
Convention de fléchage des tensions
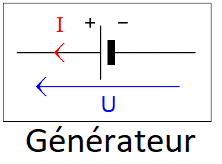
- Lorsque la tension se situe aux borne d'un générateur (batterie, pile, générateur de tension), le fléchage de la tension se fait dans le
même sens que le fléchage du courant.
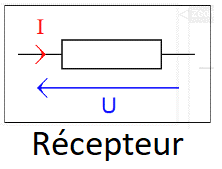
- Lorsque la tension se situe aux borne d'un récepteur (résistance, condensateur, Diode), le fléchage de la tension se fait dans le sens inverse que le fléchage du courant.
Loi des mailles
|
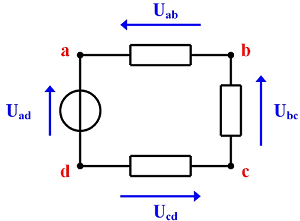
Dans un circuit électrique fermé, la somme des tensions est égales à 0.
Attention au sens des flêches!
ici:
Uad-Uab-Ubc-Ucd=0 |
Exercice 2 : Calcul de la tension aux bornes d'une résistance (loi des mailles)

Il faut faire attention aux sens des flêches en retenant que la tension est positive dans le sens de la flêche pour un générateur et dans le sens contraire pour un récepteur. On obtient donc d'après la loi des mailles: E- U1 - U2 = 0. U2 = E - U1 = 12 - 5 = 7V
Loi des noeuds
|
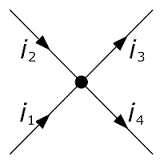
Dans un noeud, la somme des intensité qui entre dans ce noeud
est égale à la somme des intensités qui en sortent.
cela donne:
I1+I2 = I3+I4 |
Exercice 3 : Calcul de l'intensité (loi des mailles)
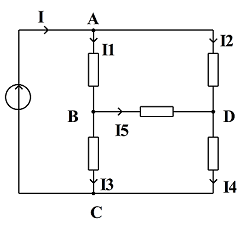
D'après la loi des noeuds, on obtient: I1= I3 + I5 Donc I5 = I1 - I3 = 30 - 20 = 10mA.
Diviseur de tension
|
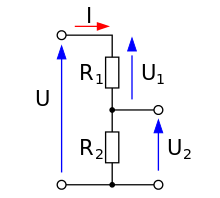
Le diviseur de tension permet d'abaisser une tension. Dans notre exemple ci-contre: U2=U. R2 R1+R2 |
Exercice 4 : Calcul de la tension aux bornes d'un diviseur de tension
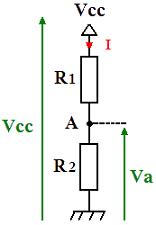
En appliquant le diviseur de tension, on obtient: Va=Vcc. R2 R1+R2 = 12. 22.103 33.103+22.103 = 4,8V
Diviseur de courant
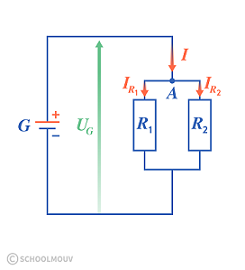
|
Le diviseur de courant permet d'abaisser le courant.
Dans notre exemple ci-contre:
IR1 = I.
R2
R1+R2
et IR2 = I. R1 R1+R2 |
Exercice 5 : Calcul du courant aux bornes d'un diviseur de courant
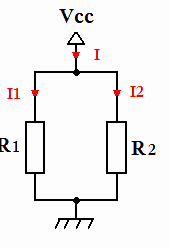
En appliquant le diviseur de courant, on obtient: Calcul de I1: I1=I. R2 R1+R2 = 10.10-3. 47.103 33.103+47.103 = 5,875.10-3A = 5,875mA. Calcul de I2: I2=I. R1 R1+R2 = 10.10-3. 33.103 33.103+47.103 = 4,125.10-3A = 4,125mA. On peut vérifier nos résultats en appliquant la loi des noeuds: On a : I = I1 + I2 = 5,875.10-3 + 4,125.10-3 = 10 mA.
Calcul de résistances équivalentes
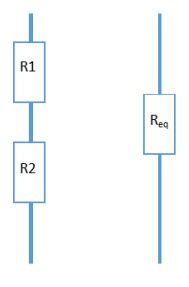
|
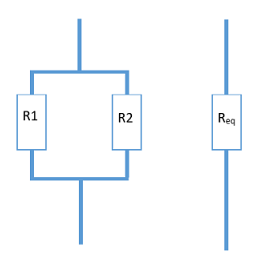
Plusieurs résistances en séries sont équivalentes à une seule de valeur égale à la somme des résistances. Req = R1 + R2. |
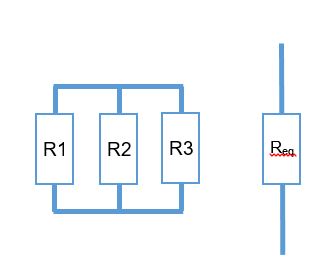
|
Plusieurs résistances en parallèles sont équivalentes à une seule de conductance égale à la somme des conductances. La conductance est l'inverse de la résistance. 1 Req = 1 R1 + 1 R2 + 1 R3 |
|
Dans le cas particulier où il n'y a que deux résistances, on a: Req= R1.R2 R1+R2 |
Exercice 6 : Calcul de la résistance équivalente au montage
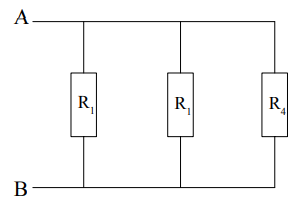
Calculez la résistance équivalente au montage sachant que R1 = 470Ω et R4=330Ω.
La puissance
Il s’agit de l’énergie échangée (donnée ou reçue) en une seconde. Elle s’exprime en Watt. P = U.I et P = R.I²
Exercices de type bac
Exercice 1
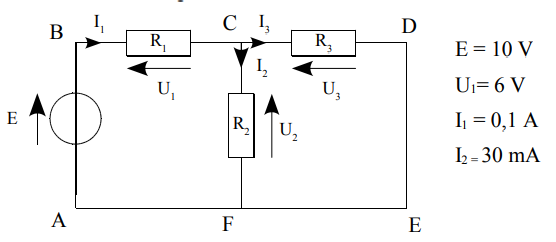
1. Etablir l'équation au noeud C. 2. En déduire la valeur de I3. 3. Établir l'équation de la maille (ABCFA). 4. En déduire l'expression de la tension U2. Calculer U2. 5. Établir l'équation de la maille (CDEFC). 6. En déduire l'expression de U3. Calculer U3. 7. Vérification de la loi des mailles : Établir l'expression de la maille (ABDEA) et montrer que E = -U1 - U3. 8. Faire l'application numérique. La loi des mailles est-elle vérifiée ?
Exercice 2
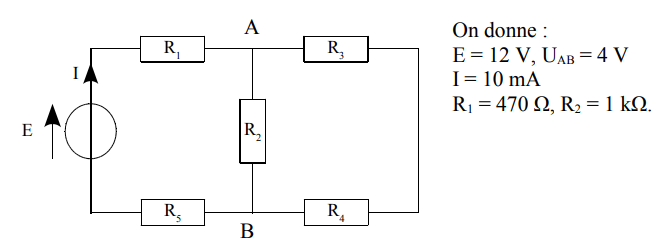
1. Recopier le schéma, flécher et annoter les différentes tensions et intensités sur le schéma (convention récepteur). Exemple : Aux bornes de R1, la tension sera notée U1 et l'intensité qui la traverse sera notée I1. 2. Quelle est la valeur du courant qui traverse R5 ? 3. Le courant qui traverse R4 a pour valeur I4 = 6mA. Calculer la valeur de l'intensité I2 qui traverse R2. 4. En déduire la valeur de I3. 5. La tension U1 = 4,7 V. Calculer la tension U5 aux bornes de la résistance R5. 6. Établir l'expression de U3 en fonction de U2 et U4. 7. Calculer U3 si U4 = 1,2 V.
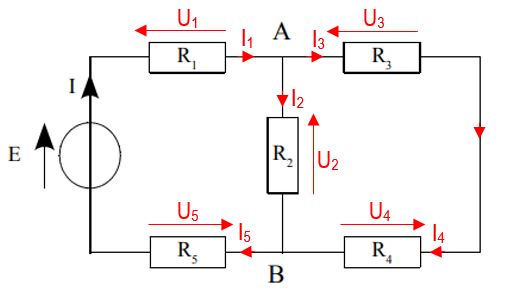
U2 = UAB donc U5 = -E -U1 - U2 = -12 - 4,7 - 4 = -20,7 V. 6. D'après la loi des mailles, on a -U2 + U3 + U4 = 0 donc U3 = U2 - U4 7. U3 = U2 - U4 = 4 - 1,2 = 2,8 V.